A process that reflects the time-evolution of an asset price. It is a stochastic process commonly used in finance to describe the evolution of traded assets over time. In the realm of derivatives, it is used for European style options and stock prices. In a mathematical form, it is expressed by the stochastic differential equation (SDE):
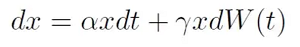
Where: α denotes the drift and γ denotes the volatility of the geometric Brownian motion process x(t).
This process is a continuous-time stochastic process in which the logarithm of the randomly varying value (e.g., a price) follows a Brownian motion (BM). Specifically, it is a non-negative variation of Brownian motion. When a Brownian Motion is geometric, the returns from the an asset trading in an active market (a stock) are compounding and stock prices cannot be negative- i.e., cannot drop below zero due to the nature of the issuers (limited liability corporations). Similar to its original version, the Brownian motion, it is a Markov process: “the future given the present state is independent of the past”
It is known for as exponential Brownian motion or for short as GBM.



Comments